树与二叉树
前置知识
- 树和图属于非线性结构(一对多),其他线性结构属于一对一(前驱和后驱唯一)。
- 树的其他表示方式:嵌套集合,凹入表示,广义表
- 树的度是节点度的最大值
- 有序树、无序树
- 森林:是 m 棵互不相交的树的集合(把根节点删除,树就变成了森林)
二叉树的逻辑结构和存储结构
- 完全二叉树的高度 h 和节点数 n 的关系 $2^{(h-1)}-1 < n < 2^h-1$ , 变形为 $h = [log_2n](向下取整) +1$ 或者 $h = [log_2 (n+1)] (向上取整)$
- 总分支数量 = 总结点数
- 叶节点数$N_0$,单分支节点数$N_1$,双分支节点数$N_2$
- 则有总结点数 $=N_0+N_1+N_2$
- 总分支数 $=N_1+2N_2$
- $N_0=N_2+1$(叶子结点数量等于双分支节点数量+1)
- 完全二叉树顺序存储结构:比如某个节点序号为 n,则其左孩子序号为 2n+1,右孩子的序号为 2n+2
- $N(总结点数) = e(边数)+1$
- $e = N00+N11+N22+……Nnn$(这两条公式都可以通过把所有分支拿到同一边来完成证明)
二叉树链式存储结构:
1
2
3
4
5
| typedef struct BTNode{
int data;
struct BTNode* lChild;
struct BTNode* rChild;
}
|
1
2
3
4
5
| typedef struct BTNode{
int data;
struct BTNode* Child;
struct BTNode* Sibling;
}
|
树与二叉树的相互转换
树->二叉树
二叉树->二叉树
遍历(分支结构线性化)
二叉树的深度优先遍历
- 前序遍历:根结点,左子节点,右子节点
- 中序遍历:左子节点,根结点,右子节点
- 后序遍历:左子节点,右子节点,根结点
- tips:可以理解为第 1/2/3 次遇到到节点时执行访问,分别对应三种遍历方式,便于理解后面递归代码实现的原理

二叉树遍历的代码实现(递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
| #include <iostream>
#include <stack>
using namespace std;
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
void preorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
stack<TreeNode*> nodeStack;
nodeStack.push(root);
while (!nodeStack.empty()) {
TreeNode* node = nodeStack.top();
nodeStack.pop();
cout << node->val << " ";
if (node->right != nullptr)
nodeStack.push(node->right);
if (node->left != nullptr)
nodeStack.push(node->left);
}
}
void inorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
stack<TreeNode*> nodeStack;
TreeNode* node = root;
while (node != nullptr || !nodeStack.empty()) {
while (node != nullptr) {
nodeStack.push(node);
node = node->left;
}
node = nodeStack.top();
nodeStack.pop();
cout << node->val << " ";
node = node->right;
}
}
void postorderTraversal(TreeNode* root) {
if (root == nullptr)
return;
stack<TreeNode*> nodeStack;
TreeNode* node = root;
TreeNode* lastVisited = nullptr;
while (node != nullptr || !nodeStack.empty()) {
while (node != nullptr) {
nodeStack.push(node);
node = node->left;
}
TreeNode* topNode = nodeStack.top();
if (topNode->right == nullptr || topNode->right == lastVisited) {
nodeStack.pop();
cout << topNode->val << " ";
lastVisited = topNode;
} else {
node = topNode->right;
}
}
}
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
cout << "前序遍历: ";
preorderTraversal(root);
cout << endl;
cout << "中序遍历: ";
inorderTraversal(root);
cout << endl;
cout << "后序遍历: ";
postorderTraversal(root);
cout << endl;
return 0;
}
|
后序遍历的代码可以根据前序遍历的代码略加更改得到。因为前序是:根左右,后序是:左右根,从而有逆后序是:根右左,相当于前序遍历的左右节点互换位置即可。
树的遍历
- 树的前序遍历和其对应的二叉树的前序遍历等价
- 树的后序遍历(也叫中序遍历)和其对应的二叉树的中序遍历等价
二叉树层次遍历和树的层次遍历(广度优先)
二叉树的层次遍历
树的层次遍历
树的考点
线索二叉树
哈夫曼树
哈夫曼树虽然是不定长编码,但是
‘树中不可能出现一个节点的编码是另一个结点的前缀,因此不用担心歧义。·
带权路径长度
- 权值越大的结点,距离根节点更近
- 树中没有度为1的结点,这类树又叫正则(严格)二叉树
- 树的带权路径长度最短
哈夫曼n叉树
如果不满足节点数等于n+k(n-1),k为正整数,则可以在前面补一个权值为0的结点,不影响带权路径长度最短的特点,也能够成功构建哈夫曼树二叉树的确定(根据遍历序列确定二叉树)
- 一个遍历序列是不可能唯一确定一棵二叉树的。至少需要两个
| 遍历序列组合 |
可否唯一确定二叉树 |
| 前序+中序 |
√ |
| 后序+中序 |
√ |
| 层次遍历+中序遍历 |
√ |
| 先序+后序 |
× |
二叉树的估计
给出遍历序列的特征情况,推断二叉树的形状
二叉树存储表达式
波兰表达式
波兰表达式摒弃括号和优先级,以遍历的方式执行运算。
例如有一个数学公式:(2-3)*(4+5)可以这样表示:*-23+45
公式中的操作符提前了,每个操作符后面跟着两个操作数,从左向右遍历就可以得到唯一的计算步骤.上图中*号后面紧邻着-号并不是操作数,其实-号代表着它会计算出一个临时的操作数tmp1作为*号的第一个操作数。因此,我们只需要把以上公式从左向右遍历一遍,就能知道该公式如何计算。编译器在将高级语言翻译成汇编代码时就是这么干的。
根据操作符的位置,波兰表达式又被称之为先缀表达式,我们平时使用的表达式称之为中缀表达式,逆波兰表达式称之为后缀表达式。
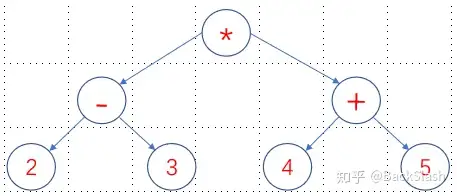
以上的二叉树称之为表达式二叉树。表达式二叉树有些特性,所有的叶子节点都是操作数,所有的非叶子节点都是操作符。这很容易理解,在基本计算单元中,操作符是核心,同时计算结果是另一个基本计算单元的操作数,反映到二叉树中,操作符既是子树的根节点同时也是另一颗子树的子节点,那就是非叶子节点。
表达式二叉树的先序遍历结果就是先缀表达式。同理,中序遍历是中缀表达式,后序遍历是后缀表达式。就像这样:
- 先序遍历: * - 2 3 + 4 5
- 中序遍历: 2 - 3 * 4 + 5
- 后序遍历: 2 3 - 4 5 + *





